AP Calculus BC: Tips and Tricks for Success!
I talk about my journey and all the resources that helped me study for the AP Calculus BC exam. Which ones are helpful, and which ones aren't all that effective? Learn more here.
Introduction
On May 2022, I took the AP Calculus BC exam (as well as the AP Statistics exam, which I’ve covered in another post). It tested limits, derivatives, integrals, applications of derivatives and integrals as well as sequences and parametric equations. I’m really proud that I got a 5 on this exam, and I wanted to share what I did and give anyone reading this blog some tips on the future.
My Experience-
AP Calculus BC isn’t that much harder than AP Calculus AB. I would say the extra units are around the same level as AP Calculus AB, provided you have a good understanding of the AB topics. The units are:
- Arc length formula
- Techniques like integration by parts
- Improper integrals (basically a combination of integrals and limits)
- Infinite sequences and convergence- Sequences were easy for me (that might be because I did math contests though).
- Parametric equations, polar equations and vector valued functions- I would say polar functions are the hardest parts of all, but really it doesn’t get much worse than “find area of [polar equation]”. Everything loops back at some point, and what you need to do is find the upper and lower bounds of integration to make sure you’re not getting the same area twice.
Some general tips are:
- Make sure you’ve got the concepts down
- If you need to memorize something (e.g. the quotient rule), make a Quizlet. Try not to make Quizlets with only a few days left to go as it really helps you more in the long run.
There are also questions that reappear quite often:
- Reoccurring questions that give you a table and ask you to find the average rate of change between 2 instants in time and then to use a Riemann sum approximation to find the area under the curve.
- At least 1 question will ask you for the average value formula for an integral
- Q6 involves sequences, make sure to study those last few units!
- At least one question involves parametric equations. The exam might ask you to give the velocity vector of a certain particle at a certain point in time, given x(t) and y(t).
- A graphical representation of a function. The question asks you to take the derivative or integral without using a calculator.
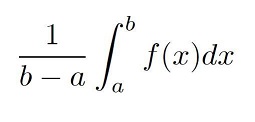
How I Studied + Advice
I didn’t really start studying until the middle of April, when I was done with all the content. In retrospect, this was my biggest mistake as I didn’t have the time to study as much as I wanted. I would recommend you try to get ahead of the class and make a plan so you’ll be done by the end of March, giving you extra time to study. That way, you don’t have to cram right at the end.
At the very beginning, I would recommend you use your textbook for problems (my textbook was Calculus: Graphical, Numerical, Algebraic), and Khan Academy’s videos are great if you’re struggling with a particular topic. However, the problems are too surface level and plug and chuggish for the AP exams.
I know this sounds obvious but the best resource is the AP Calculus BC practice exams. You can find them at edufilestorage.com.The multiple choice questions are easy and are good practice if you’re starting out.
The free response questions are harder, but as long as you know your stuff, the applications are actually very obvious. What I really appreciate is that they specifically tell you what you need to include (e.g. to get this mark, you need to include the notation, the constant of integration, etc.) so you can easily correct your mistakes.
If you need additional practice, you can use CrackAP.com as they have multiple choice and free response problems. You can also look at https://tutorial.math.lamar.edu/Classes/CalcII/CalcII.aspx.
One of the formula sheets I used to quickly review was https://www.dvusd.org/cms/lib/AZ01901092/Centricity/Domain/2903/BC%20cram%20sheet.pdf. You’re also allowed a calculator, and you might need it to evaluate some integrals that you can’t figure out how to use normally. I’ve also used it to find the zeroes of certain functions (particularly in critical point problems).
And finally, if you have any time left, there are many great above and beyond resources, such as MIT OCW 18.01, which includes a few other topics like trigonometric substitution or AoPS’s Calculus book.